Quadratic Functions from Vieta's Theorem
- Math Space BP. Malaysia
- Sep 17, 2022
- 4 min read
Abstract|
A fantastic fuctions that occur surrounding us. How did it work and is it completely same with what we learn from syllabus? Here to find out the relationship between quadratic functions and Vieta's Theorem.
Have you ever heard about Vieta's Theorem before? I am sure you did or you may know it when you are studying additional maths. It can be said that we are surrounded by these kinds of mathematics questions, such as chicken and rabbit cage, the mathematics question that occurred from ancient China in the 15th century and yet just like Vieta's Theorem.
Just like its name, Vieta’s Theorem was discovered by Franciscus Vieta, a French mathematician in the 16th century. He was once a lawyer who worked as a privy councillor for both kings, Henry III and Henry IV of French. He studied in the field of algebra and proved the development of algebra. And now, you must have a question about what Vieta's Theorem talks about.
WHAT IS VIETA’S THEOREM
Commonly, Vieta’s Theorem are formulas that relate the coefficients of a polynomial to sums and products of its roots. Now, I guess you must be confused by this kind of explanation. Let’s change another explanation that you are familiar with. You may know about the formula ax^2 + bx + c = 0 and a≠0 whether you learn maths or additional maths. For the ones learning additional maths, you may find out another equation which in the same topic in the syllabus, yet 2 roots satisfies with the relationship of :
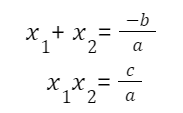
This is Vieta’s Theorem for quadratic polynomials, whatever it is a>0 or a<0 , it is proof. Now, did you get it?
THE APPLICATION OF VIETA’S THEOREM
Everything has its significance to exist, undeniable the quadratic equation too. We use quadratic functions to determine a product’s profit or formulating the speed of an object in daily life. On the other hand, we use it to calculate the areas as well. Besides, it also plays an important role in numerous physical and mathematical problems that exist in the form of quadratic equations.
EXAMPLE IN SOLVING QUADRATIC QUESTION BY VIETA’S THEOREM
To quote an example, x^2 + 8x +12 = 0 , you may get a few minutes to try this before we proceed to the solution if you will. Try to guess how much solution we can use to solve this question.
First , we can apply Vieta’s Theorem that I mentioned just now. By using this method we can simply guess the numbers of roots if we drag in
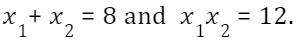
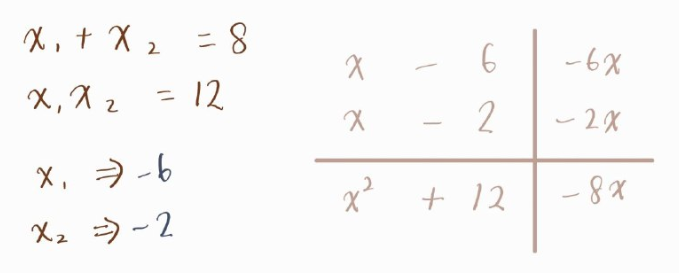
Or we can use the quadratic equation of one unknown that we studied before too, yet
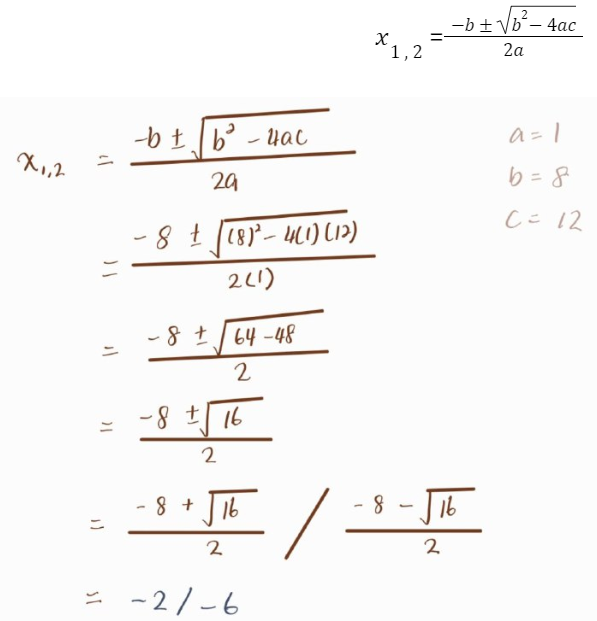
Instead of these, we may use another equation which is carried out by Po-Shen-Loh , a famous American professor of mathematics at Carnegie Mellon University and the national coach of the United States’ International Maths Olympiad Team.
The method is like this, starting with Vieta's Theorem , we will know that the average of
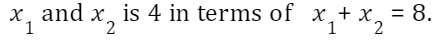

Besides that, we must ensure that (4-u) times (4+u) will be 12.
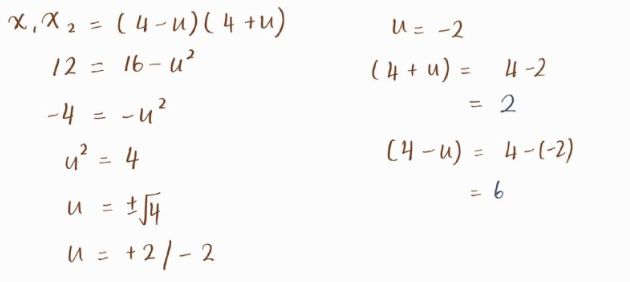
By using this solution, we might no need to guess the roots by using the first formula and no need to remember the complicated quadratic equation of one unknown just like the second solution. By the way, we can simplify our calculations too.
QUADRATIC EQUATION OF THE ONE UNKNOWN UNDER THE VIETA’S THEOREM
In fact, the quadratic equation of the one unknown that we use in the second solution is proof to be the transition of Vieta's Theorem. It can be said that it is the other form that expresses Vieta’s Theorem.

Therefore, we can know that Vieta's Theorem can be derivative to many forms and the quadratic equation of one unknown is one of them.
We can simply use this formula when we have a direct number of a, b and c. But if there is an answer of roots and the unknown in the equation, then we have to use the relationship to find the unknown instead of using the formula. To quote an example, given that the roots of x^2 + (3y-1)x + 4y = 0 is -2 and -6, find the value of y.
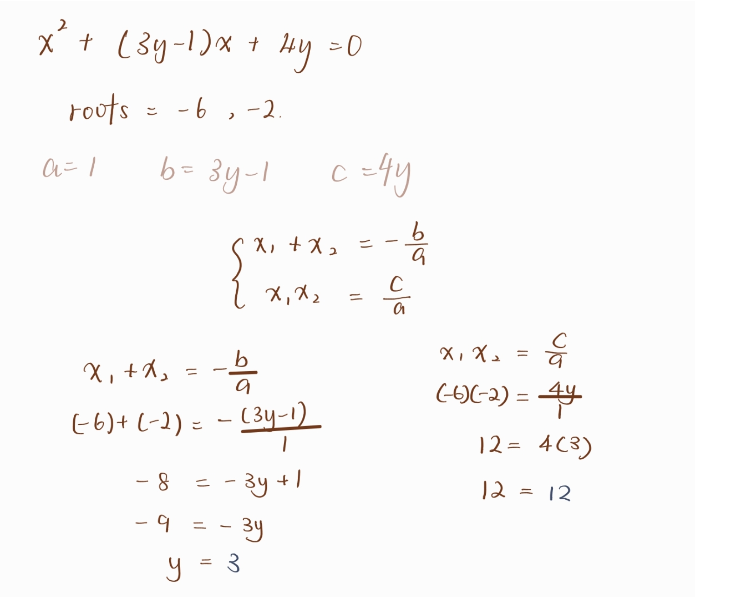
Now, you may be clear whether we should either use formulas or the relationship of quadratic functions in solving the question.
VIETA’S THEOREM IN CUBIC EQUATION
Cubic equation was written in the form of ax^3 + bx^2 + cx + d = 0.
With the fundamental theorem of algebra, which was discovered by Carl Friedrich Gauss, we may know that xn = n roots. Therefore, it might be 3 roots in a cubic equation.
So, there is the question how to write the relationship by using Vieta’s Theorem.
According to the relationship in quadratic equation, we may proof that:

CONCLUSION
As a conclusion, we may know that the denominator for the relationships is always a and the numerator are written according to the order where start with b , c and follow with d. Other than that, we can conclude that the symbol starts with negative and follows with positive.
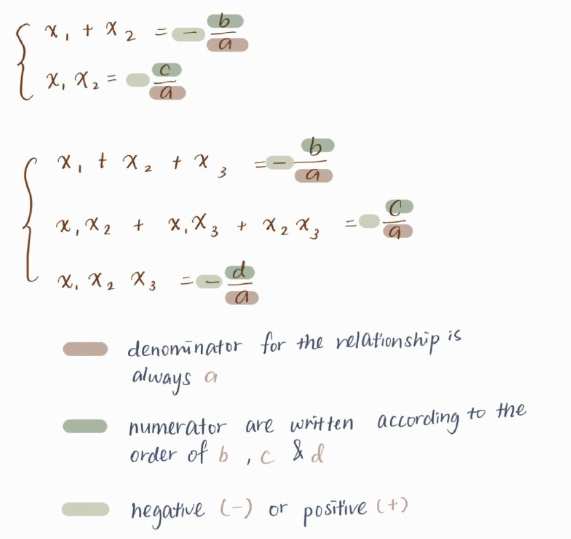
Now, you may know Vieta's Theorem. If you have time, try to think about the relationships of the quartic equation of one unknown using the rules of Vieta’s Theorem.
Hope you can enjoy the joy while solving the question.
References :
AUTHOR

TEO SAMMI
A girl who like reading and writing.:)



Comments