The Holy Grail of Mathematics
- Math Space BP. Malaysia
- Oct 22, 2022
- 3 min read
Abstract|
As one of the most important unsolved problems in Mathematics, the Riemann Hypothesis has stumped mathematicians for centuries. This article introduces the Riemann Zeta function which is the key to the hypothesis and its mesmerising connection to prime numbers.

What is the most difficult way to become a millionaire? Well, mathematicians have a
unified answer for this: conquer the Riemann Hypothesis! As one of the Millennium Prize
Problems, the Clay Mathematics Institute offers 1 million US dollars for whoever proves (or
perhaps disproves, though very unlikely) the hypothesis.
Unlike Fermat’s Last Theorem and the Four Colour Theorem, the hypothesis itself requires knowledge in complex analysis and non-mathematics students might find it tough to understand. Here is the statement: all non-trivial zeros of the zeta function have real part one-half. Obviously, it would be impossible for me to provide a full analysis of the statement. What I can do here is to introduce the
Riemann Zeta function (the key to the hypothesis) and also explain its relationship with
another interesting area of Mathematics – prime numbers.

I shall start by introducing the famous Basel Problem: find a closed form for the sum
of infinite series of reciprocal squares.
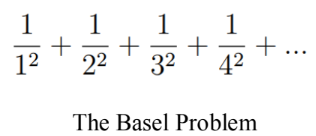
The problem was first posed by Pietro Mengoli in 1650. Note that the series is converging,
and mathematicians at that time tried really hard to find a closed form, i.e., an exact value for
it. It was Leonhard Euler who finally solved the problem by providing a surprising answer:
π^2/6. Yes, this is the mathematical constant π that we define as the ratio of the circumference of
a circle to its diameter and has an approximate value of 22/7. We are not going to discuss
Euler’s solution in detail as it deserves another article for it.
Later in 1859, Bernhard Riemann proposed his hypothesis by using what is known as
the Riemann Zeta function today. Instead of squares, Riemann allowed the exponents to be
any real value greater than 1. This is how it looks like:
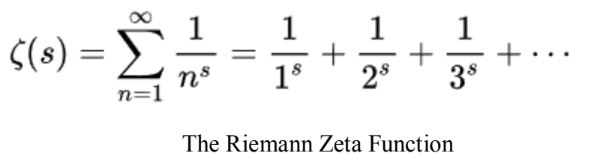
Note that when s=2, the Riemann Zeta function is simply the Basel Problem. What Riemann
noticed from this function is that it reveals some of the underlying properties of prime
numbers that could enable us to predict the distribution of prime numbers. The mathematical
tools behind his discovery are too advanced to be included here. However, I can illustrate the
elegant connection of the function with prime numbers by using an ancient method known as
the Sieve of Eratosthenes.
Around 230 B.C.E, Eratosthenes found a way to find prime numbers effectively. First,
we list down all natural numbers from 2 to say, 50. You can of course choose any number
higher than 50.
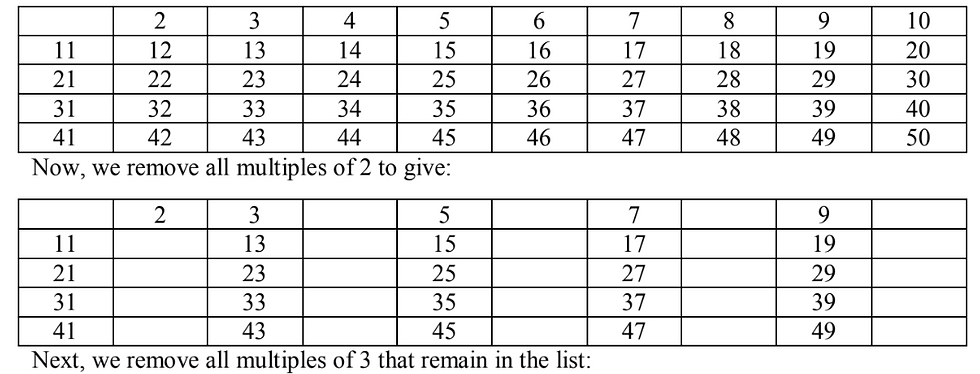
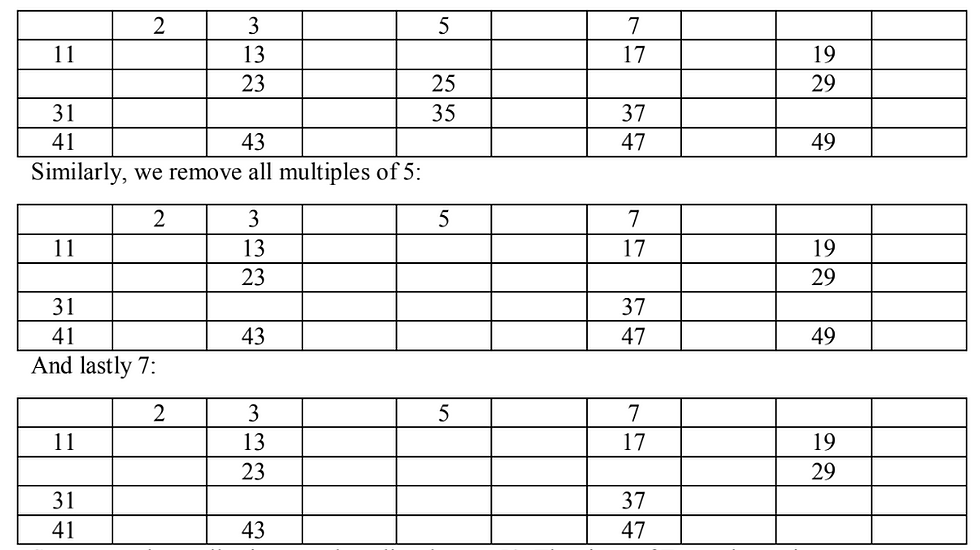
So now we have all prime numbers listed up to 50. The sieve of Eratosthenes is a
straightforward yet useful tool to find prime numbers and we shall discuss its connection with
the Zeta function in our next paragraph.
Leonhard Euler (again) managed to find a way to link the Sieve of Eratosthenes and
the Riemann Zeta function. To understand how he did that, I need your patience to go
through a little bit of high school algebra:

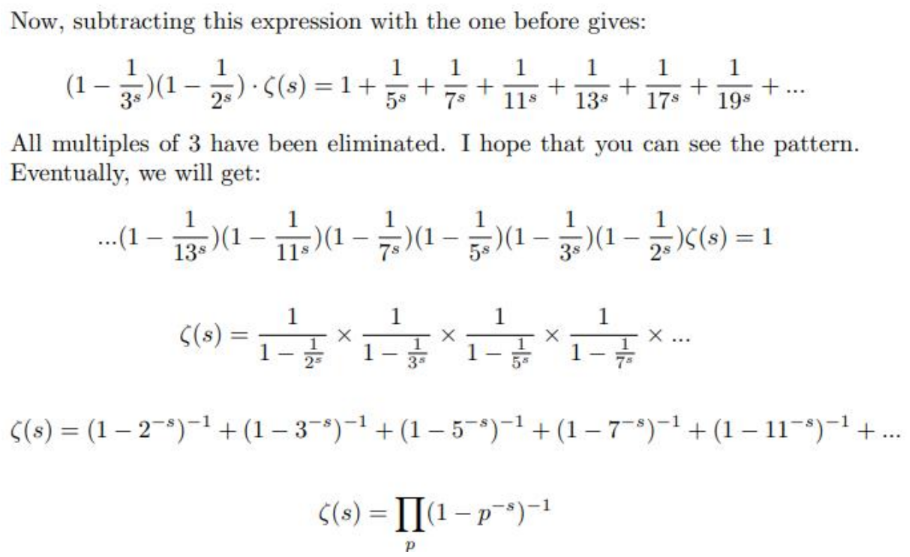
And we get what John Derbyshire called as “The Golden Key” in his award-winning book.
Notice how the infinite sum on the LHS is equal to the infinite product involving prime
numbers on the RHS. This is the beauty of prime numbers that I wanted to show you.
If you are still with me, congratulations on being a step closer to understanding the
Riemann Hypothesis. Though this is only the very first step, a journey of a thousand miles
begins with a single step. In fact, a mathematician would be considered crazy by his
colleagues if he were to devote his entire life to the hypothesis. But somehow, we still need
someone “crazy” like Andrew Wiles who solved Fermat’s Last Theorem, to one day unravel
mysteries behind the Riemann Hypothesis and the distribution of prime numbers.
Reference:
Prime Obsession by John Derbyshire
https://en.wikipedia.org/wiki/Riemann_hypothesis
https://en.wikipedia.org/wiki/Bernhard_Riemann
AUTHOR

LAI WEI SIANG
Wei Siang is currently doing his A-level study at Kolej Yayasan UEM under the sponsorship of JPA. Being a math maniac, he aspires to pursue Mathematics as his degree course in the UK. Inspired by “the unreasonably effectiveness of Mathematics” in explaining our universe, he is determined to one day unravel mysteries in the field through rigorous mathematical research.



Comments