Logarithms

HISTORY OF LOGARITHMS

Abstract|

A brief introduction of logarithms, its history and its application.

This concept was published first in 1800 BC form a well-known civilization on the Euphrates River

which called Babylon. Babylonians were especially brilliant with mathematic, science ,astronomical

and architecture. After some archaeologist study the history of Babylon, they discover many clay

tablets. Some of the clay tablets had some record some number like this:

And the number on the clay tablets are probably like this:

As you know every scientist will be interested when they had seen those numbers. They started

investigate the function of those number. Luckily, one France’s scientist who called Nicolas Chuquet

discovered that the different between each upper numbers are +1 however the different between

each bottom numbers are +2

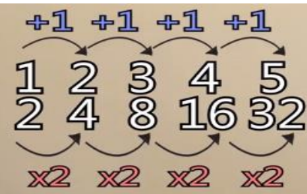
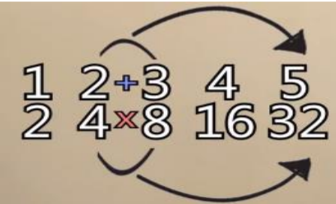
He also discovered that the sum of two upper number will equal to the product of two bottom

number.

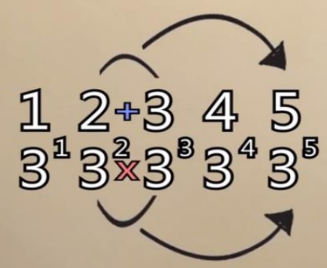
Until the 1554s, another Germen scientist who called Michael Stiefel he convert the base of the

index numbers from 2 to 3 and he found that the law still remain unchanged

When 1614s ,a Scotland astronomer who called John Napier decided to find a way to simplify his

complex calculate in the astronomy. Then his found the index numbers and study about it. After the

research he publish a book named Mirifici logarithmorum canonis descriptio. In this book, John

Napier invented Log with base 2

After that, an English mathematician who call Henry Briggs introduced common logarithms in base

10, which were easier to use and tables of logarithms were published in many forms over four

centuries.

Laws of Logarithms

An equation in index form can be written as N=a^x where a>0 and a not equal to1.N,a and x are

variables. We can find the value of one variable if the value of the other two variables are given.

For example,

a) If 81 = 9^x , then x = 2

b) If 1000 =a^3, then a = 3√1000 = 10

c) If N =5^3, then N=125

Then, the relationship between equations in index and logarithmic forms can be defined as follows:

loga N = x same as N = a^x where a> 0 and a is not equal to 1

From the definition above, it can be concluded that :

If a^0 = 1 , then loga 1 = 0

If a^1 = a , then loga a = 1

Based on the definition of logarithms of a number, we can convert an index equation to the

logarithmic for

The power of the index number is the logarithmic value

The base of the index number is the base of the logarithm

Otherwise, we can also convert an equation in logarithmic form to index form

Applications of Logarithms In Real Life

i) Logarithms are used for measuring the magnitude of earthquakes

The Richter Scale - Earthquakes are measured on the Richter Scale, which is a base 10

logarithmic scale. This scale measures the magnitude of an earthquake, which is the amount of

energy released by it. For every single increase on this scale, the magnitude is increased by a

factor of 10.

ii) Logarithms are used for measuring the noise levels in dBs (decibels)

In decibels, this ratio is expressed by taking its logarithm (to base 10) and multiplying by 10. For

example, if V-OUT = 4 V and V-IN = 0.5 V, the gain is 4/0.5 = 8. Expressed in decibels, this is: Because the decibel scale is a logarithmic one, doubling the gain does not double the decibel value.

iii) They are used to measure the pH level of chemicals

The precise definition of pH is "the negative common logarithm of the activity of

hydrogen ion in solution". For practical purposes, the activity is approximated as

concentration in moles/L: pH = - log 10 ([H+]) .

iv) They are used to measure the radioactivity, mainly to detect the half life of a

radioactive element

A log of a borehole obtained through the use of gamma, neutron, or other radioactivity

logging methods. ii. The generic name for well logs whose curves derive from reactions of

atomic nuclei involving the behaviour of gamma rays and/or neutrons.

Conclusion

In my opinion, I think logarithm is absolutely useful in our life. It will lets us work backwards

though a calculation. It lets us undo exponential effects. Beyond just being an inverse operation,

logarithms have a few specific properties that are quite useful such as it is a convenient way to

express large numbers.

Every coin have two sides, there are also some weakness in logarithms. Logarithms is one

material that is difficult for student. There are several causes of students’ difficulties in

understanding logarithms, namely lack of understanding about logarithmic definition, lack of

ability to see the relation of facts to matter or too focused on the memorizing facts and

procedural.

To solve those problem, student can do some research about logarithms and do more practise

to learn more about logarithms properties because practise make perfect.

---

Reference

i) https://www.youtube.com/watch?v=00cVSGycCGQ

ii) https://en.wikipedia.org/wiki/History_of_logarithms

iii) https://maths.wizert.com/blog/the-different-applications-of-

logarithms#:~:text=Logarithms%20are%20used%20for%20measuring,the%20pH

%20level%20of%20chemicals.&text=Logarithms%20are%20used%20in%20radioa

activity,life%20of%20a%20radioactive%20element.

---

AUTHOR

TENRY TAN

My name is Tenry Tan, study in SMK Dato Bentara Luar. I am glad to write this math article. I hope you all will enjoy to read it.