A Glimpse into Prime Numbers
- Math Space BP. Malaysia
- Oct 15, 2022
- 3 min read
Abstract|
As the building blocks of natural numbers, prime numbers exhibit some of the most fascinating patterns for mathematicians. This article provides insights into Euclid's work on the infinitude of prime numbers, the Fundamental Theorem of Arithmetic, as well as the application of prime numbers in our daily life.
What do 127, 8191 and 131,071 have in common? You may have guessed it right
from the title: they are all prime numbers. In addition, they are primes in the form of 2
^n − 1,which are also known as Mersenne Primes. For example, 127 is 2^7 − 1 and 8191 equals 2^13 − 1. While they may seem odd to you, mathematicians love to investigate their
properties, and tons of theorems have been developed since they made their first appearance
in Mathematics.

Recall that a prime number is a positive integer whose factors only consist of 1 and
itself. By definition, a prime number has two positive divisors. Hence for this specific reason,
I hope you recognise that 1 is not a prime number because it has only 1 positive divisor.
Another thing to note is that 2 is the only even prime. This is obvious because every even
integer greater than 2 is divisible by at least 3 factors: 1, 2 and itself. Therefore, they must be
composite numbers, i.e., not prime.
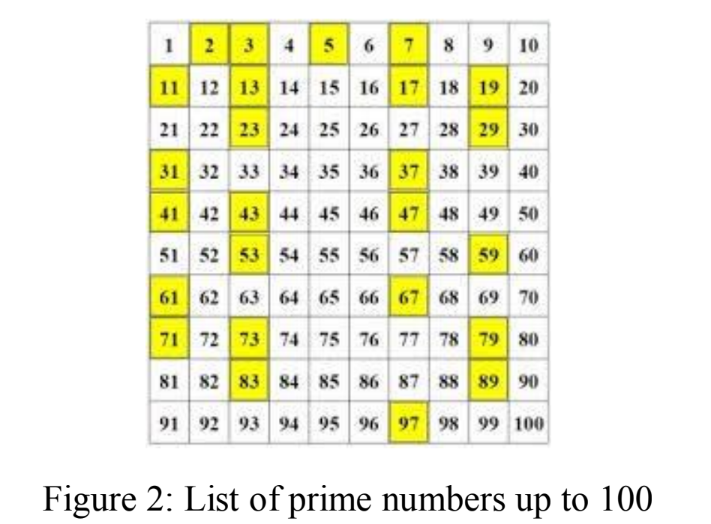
The study of prime numbers dates back to 300 BCE, when a Greek mathematician,
Euclid of Alexandria proved the infinitude of prime numbers. His proof is easy to understand,
yet it lays the groundwork for future research in prime numbers. I shall present the proof in
LaTeX:

Figure 3: Euclid’s Proof of the infinitude of prime numbers
This also implies that we can never find the largest prime number. However, this fact does
not stop mathematicians from searching for larger primes. In fact, the largest known prime
today is a Mersenne Prime and it has 24,862,048 digits.
Despite being the building blocks of natural numbers, prime numbers have tantalized
mathematicians for centuries because of their unusual behaviors and patterns. To explain why
prime numbers are of the utmost importance, we have to introduce the Fundamental Theorem
of Arithmetic. The theorem states that every integer greater than 1 can be expressed uniquely
as a product of prime numbers. Remember doing prime factorisation in high school math?
Thanks to the theorem, we know that prime factorisation works for every integer greater than
1. Hence, prime numbers are important in Mathematics just as how atoms are in Chemistry.
That is why mathematicians believe that if we could unravel the profound mysteries behind
prime numbers, we could revamp our understanding of Mathematics itself. An example of the
mysteries is the Riemann Hypothesis. As one of the Millennium Prize Problems, the problem
remains unsolved for more than 150 years. Whoever solves it will not only get one million
US dollars but also achieve immortality in Mathematics.
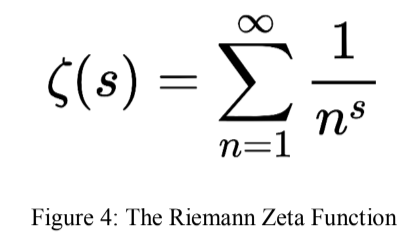
Whether you realise it or not, one of the most important applications of prime
numbers is cryptography. Today, cryptography is inseparable from our life as we are
constantly dealing with digital information. But how exactly prime numbers protect
encrypted data? Here is a simple analogy: Before sending data to cyberspace, a sender can
encrypt the data by multiplying two prime numbers that are often very large. The data can be
deciphered by breaking down the composite number into two prime numbers again. Only the
receiver knows the exact prime numbers used by the sender. Because there are infinitely
many prime numbers, it is almost impossible for a hacker to break down the number. It is this
property of prime numbers that ensures the safety of your online transactions and keeps
hackers at bay.

Recently, a number theorist who works in the theory of prime numbers, James
Maynard was awarded the Fields Medal (the Nobel Prize of Mathematics) for his
contributions to analytic number theory. However, given that the greatest minds of the world
struggle to solve prime-related problems, he mentioned in an interview that “we still poorly
understand the basic properties of prime numbers.” Therefore, there is still a long journey to
go before we can finally be successful in “taming” prime numbers. At the same time, we
could also expect more treasures of the field to be discovered in our journey to reveal the
underlying mysteries of prime numbers.
Reference:
https://www.ck12.org/c/arithmetic/prime-and-composite-numbers/rwa/Prime-Protection/
https://en.wikipedia.org/wiki/Prime_number
https://en.wikipedia.org/wiki/Mersenne_prime#:~:text=In%20mathematics%2C%20a%20Me
rsenne%20prime,so%20is%202n%20%E2%88%92%201
AUTHOR

LAI WEI SIANG
Wei Siang is currently doing his A-level study at Kolej Yayasan UEM under the sponsorship of JPA. Being a math maniac, he aspires to pursue Mathematics as his degree course in the UK. Inspired by “the unreasonably effectiveness of Mathematics” in explaining our universe, he is determined to one day unravel mysteries in the field through rigorous mathematical research.




Comments