Have you ever thought that dividing some numbers by zero? Or did you even come across any mathematical questions of x/0 ?
What you will notice is, that when you divide x by zero, and press it into the calculator, you will get a math error?
Try to model it using simple situations, imagine you have 10 apples, how can you divide among 0 students? You could not even do that! And therefore, to keep it simple, you will not get any answer when dividing x by zero! Let’s take a deeper look into it!
Normally, when we divide numbers by smaller and smaller numbers, you will get a bigger and bigger number!
Eg.
10 divide by 5 = 2
When the number gets smaller and smaller,
10 divide by 2= 5
10 divide by 1=10
10 divide by 0.1= 100
10 divide by 0.01=1000
etc...
Therefore, it is clear that when a number divides by smaller numbers, it tends to be bigger and bigger, even reaching infinity at the end!
Graph proving
If you plot into a graph, you will notice that it forms a reciprocal graph! The y-value, which is the value you get after the division tends to be bigger and bigger while the x value, which is your divider tends to be smaller and smaller. So, can we conclude that
10 / 0 = Infinity ?
No! It is incorrect.
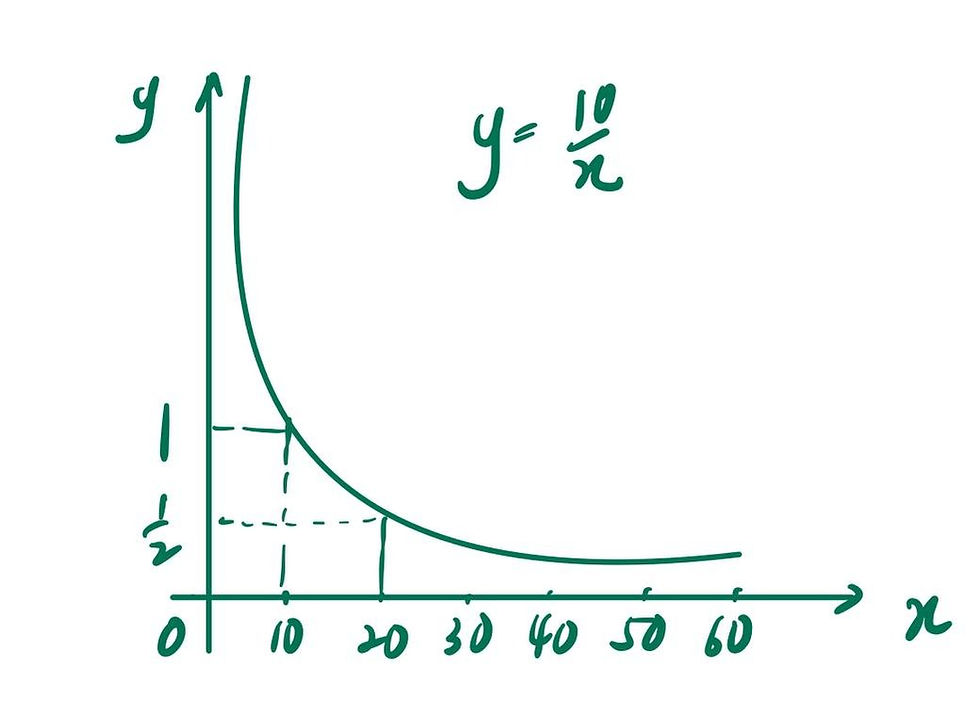
Based on the graph, we could not only conclude that when the x value approach 0, the y-value approaches infinity? But it does not mean that when x=0, y=infinity as the graph never touches on the y-axis, where x=0.
Try to think about, when we are walking towards the school, is approaching the school (you are still 100 metres away from school) the same thing as you are at school? No! So, it is really important that you make clear the difference between ‘’approaching’’ and ‘’exactly at’’.
To delve deeper, let’s take a closer look at what division really means.
10 / 2can mean how many times you need to add 2 to get 10, and it also means 2 * ?=10
Eg.
10 / 2 =5
means
2+2+2+2+2=10
also means 2* 5=10
That is the beauty of maths! where you can express the same thing in a different pattern!
Let’s take a look at the‘’ multiplicative inverse of number’’
For your information, multiplication means the inverse of division and vice versa.
For example,
2 * 5= 10 and 10*1/5 = 2
The multiplicative inverse of 5 is 1/5.
So the formula is :
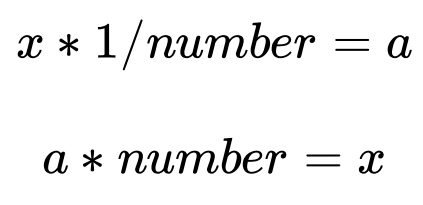
And you will get the same thing back after multiplying the inverse of that number.
Moving on,
As you might notice, the product of any number and its multiplicative inverse is always 1.
5 * 1/5 =1
3 * 1/3 =1
2* 1/2 =1
So if we want to divide by zero, according to the previous proving,
1/0 * 0 should be 1 as well (technically).
However, as we know, you will always get zero when you multiply any number with 0! Therefore, the first proving method shows that 1/0 do not exist and any number could not divide by zero! And zero do not have multiplicative inverse as well.
But what could we do when we meet 1/0 during our calculation? Let become a one-day mathematician and try to assume 1/0 = infinity.
Going back to the multiplicative inverse rule,
Since technically
1/0 * 0 =1
Infinity *0 =1
Let’s say
(Infinity *0) + (Infinity *0)=2
When we factor out,
(Infinity) (0+0)=2
(Infinity) (0)=2
Infinity *0=1
1 is not equal to 2!
Therefore, we prove again that 1/0 will never exist and there is no valid answer for that!
Application in SPM Integration
I believe that you have met this integral before:
1) Integrate the following integral
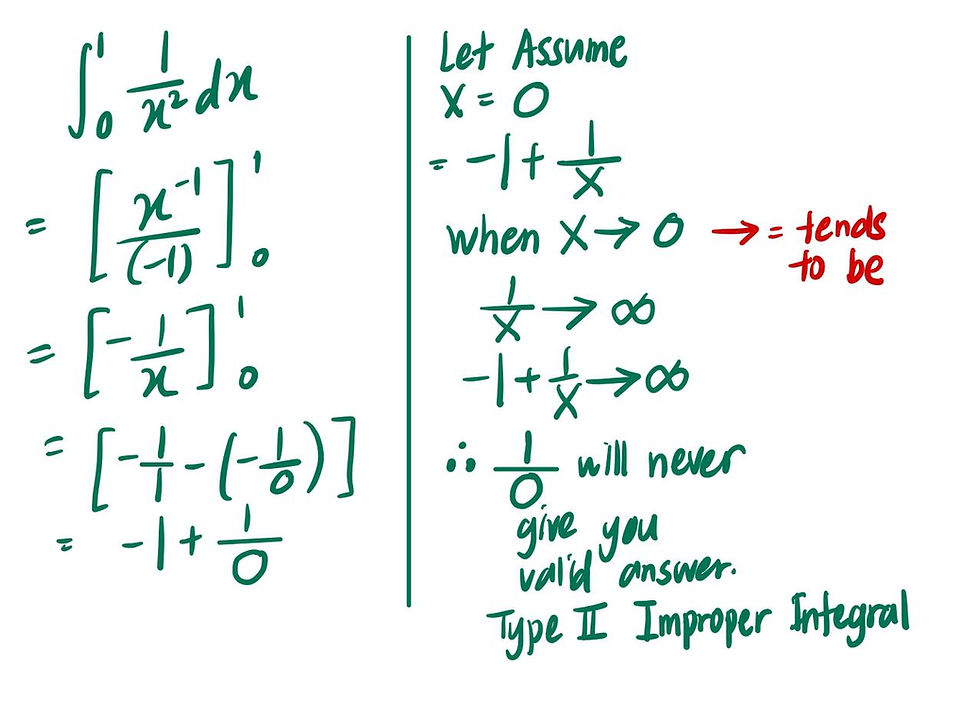
It clearly shows that whenever 1/0 appears in your working, you will not get any final valid answer!
Reference:
OUR AUTHOR
HENRY TAN
Henry is a Yayasan Khazanah Scholar from Batu Pahat , Johor, currently doing A Levels at Kolej Yayasan UEM. He hopes to pursue Actuarial Science as his degree at top universities in the UK or US one day. With a high enthusiasm for economics, he expresses his views through economics essay writing and follows the Instagram page of The World Economic Forum as his morning reading. Meanwhile, he is also a math lover and is actively involved in tackling the education inequality for mathematics subjects in his hometown.
Comments