|Abstract:
It has always been our dream to predict the future with great accuracy. This article looks into the thoughts of several big names as well as the discovery of the famously known Butterfly Effect and its potential to refute the idea of absolute determinism.
Do you believe that the flap of a butterfly’s wings in Brazil could create tiny changes in
the atmosphere and eventually lead to a tornado in Texas? The idea behind this question is the
famous Butterfly Effect, in which a slight change in the initial system may cause a dramatic change in the final outcome. We call these systems (like the weather and motions of planets) chaotic. Today, we have a branch of Mathematics called The Chaos Theory to investigate these chaotic systems.
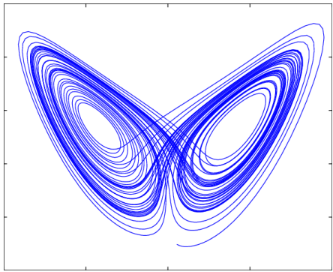
Figure 1: The Butterfly Effect in Lorenz System
However, the theory only begins to gain traction after the 1960s. The reason is that we
were quite successful in predicting the occurrence of natural phenomena (like eclipses) and
planetary motions by using Newtonian Physics, namely Newton’s laws of motion and Newton’s law of universal gravitation. Everything seemed to be predictable if we could apply our knowledge in science.
A French mathematician Pierre-Simon de Laplace then came up with a famous thought
experiment in 1814. If someone knows the precise location and momentum of every atom in the
universe, their past and future values for any given time are entailed. In other words, the future is
totally deterministic and governed by the laws of classical mechanics.
Another big fan of absolute determinism is none other than the greatest physicist of the
20th century, Albert Einstein. He believed that the universe is governed by sets of physics laws, and there is no role for probabilities and uncertainties to come in. This is why he refused to accept
quantum mechanics (as in his famous quote: “God does not play dice!”), and it turned out to be one of the biggest mistakes he had ever made.
Figure 2: Albert Einstein once said: “God does not play dice!”
The idea of absolute determinism was challenged in the 1960s when an American
Meteorologist, Ed Lorenz, discovered something unusual in his daily weather prediction, though it
was perhaps a pure coincidence. In his time, people used a numerical computer model to simulate
the weather. There were 12 equations and 12 variables like temperature and air humidity to be
inputted into the computer. One day, Lorenz decided to rerun the computer for verification purposes, but this time he took a shortcut by using the result from the middle of the previous run. To his surprise, the result printed out by the computer was a completely different weather scenario!
Figure 3: A weather simulation
Initially, Lorenz thought that his computer had broken down. Later, he realized the
‘culprits’ were the rounded-off values he took for the second run. How can these tiny changes have
such a significant effect on the outcome? He then repeated his experiment, but this time in a
convection model where only 3 equations were involved. Yet, he found the same pattern again: a
tiny change in the initial condition causes a dramatic change in the final outcome.
Take the three-body problem as another example. In the 19th century, Henri Poincare
mathematically showed that there is no simple solution for the three-body problem and even the
slightest change in the initial positions of the objects may cause a completely different result.
Figure 4: The Three-Body Problem
These discoveries raise the question: is the FUTURE really PREDICTABLE? Obviously, it
would be impossible for humans to have their measurements with perfect accuracy, and what I
mean by perfect accuracy is infinitely many decimal places. So next time, don’t blame the
meteorological department for inaccurate weather forecasts!
References:
https://www.youtube.com/watch?v=fDek6cYijxI
https://en.wikipedia.org/wiki/Butterfly_effect
https://en.wikipedia.org/wiki/Chaos_theory
OUR AUTHOR
LAI WEI SIANG
Wei Siang is currently doing his A-level study at Kolej Yayasan UEM under the sponsorship of JPA. Being a math maniac, he aspires to pursue Mathematics as his degree course in the UK. Inspired by “the unreasonably effectiveness of Mathematics” in explaining our universe, he is determined to one day unravel mysteries in the field through rigorous mathematical research.
Comments